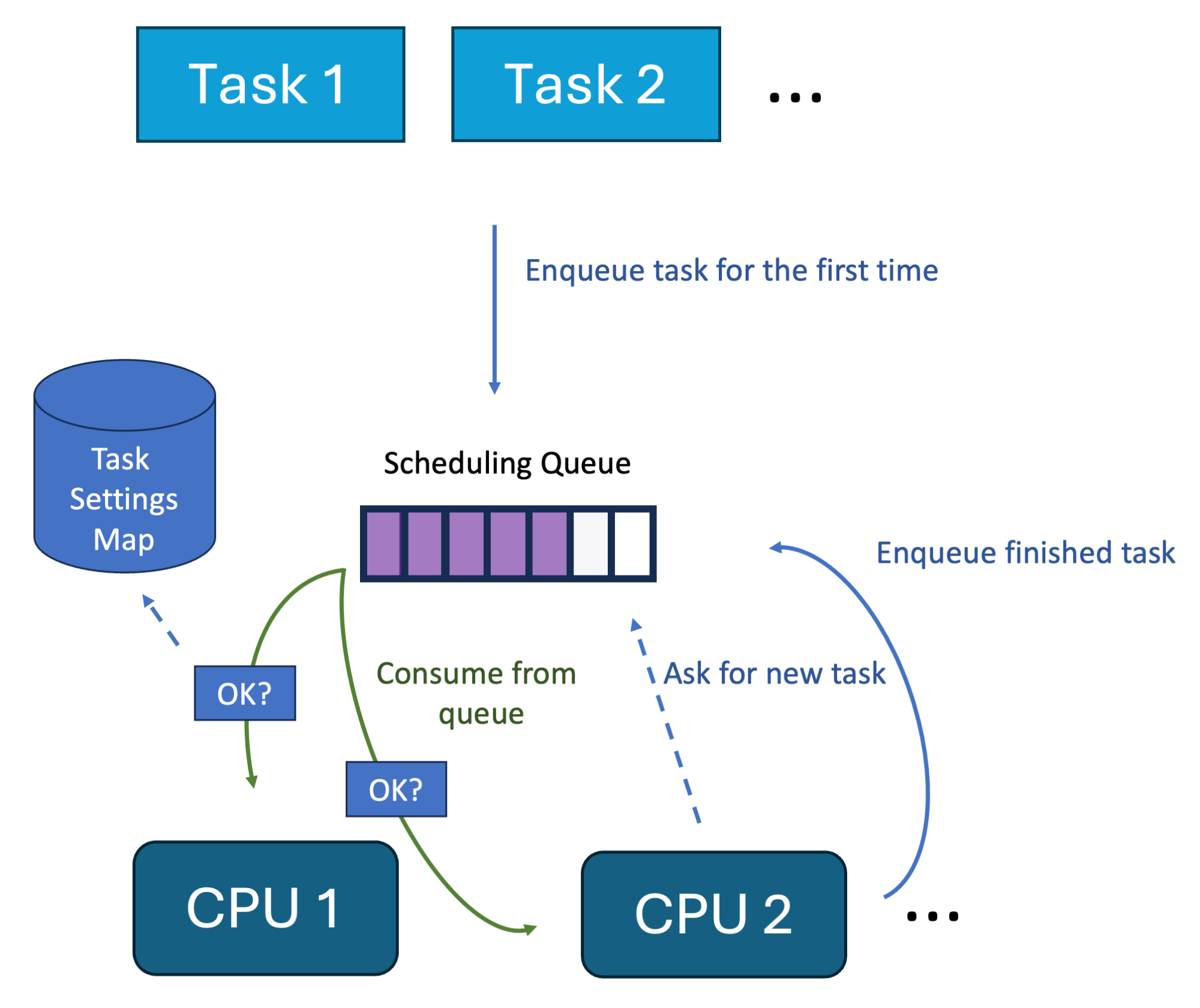
Welcome back to my hello-ebpf series. Last week, I showed you how to create a custom Linux scheduler with a simple web API to control the task scheduling using sched-ext. Just so you know: A talk based on this blog post got accepted in the Testing and Continuous Delivery dev room at FOSDEM 2025. But this is not what I’m going to talk about in this blog post; instead, this article is on a topic that I covered almost exactly eleven years ago on this very blog: Lottery scheduling. We’ll extend the taskcontrol project covered in last week’s post with a new scheduler.

Foundations and Retrospektive

Eleven years ago, I was a student in Professor Frank Bellosa‘s operating systems course, learning about different schedulers. I wrote a blog post on a scheduler that I found particularly interesting: the lottery scheduler. I could write a new introduction to lottery scheduling, but I can also delegate this task to my old self:

I currently have a course covering operating systems at university. We learn in this course several scheduling algorithms. An operating system needs these kind of algorithms to determine which process to run at which time to allow these process to be executed “simultaniously” (from the users view).

Good scheduling algorithms have normally some very nice features:

• They avoid the starving of one process (that one process can’t run at all and therefore makes no progress).
• That all processes run the approriate percentage (defined by it’s priority) of time in each bigger time interval.

But they are maybe not only useful for operating systems but also for people like me. Probably they could help me to improve the scheduling of my learning.

An algorithm that seems to be suited best for this purpose is called lottery scheduling (pdf). It’s an algorithm that gives a each process some lottery tickets (their number resembles the priority of the process). Every time the algorithm has to choose a new process to run, it simply picks a lottery ticket randomly and returns the process that owns the ticket. A useful addition is (in scenarios with only a few tickets) to remove the tickets that are picked temporarily from the lottery pot and put them back again, when the pot is empty.

Real life practice in lottery scheduling

We can visualize this similarly to the FIFO scheduler from last week’s blog post:

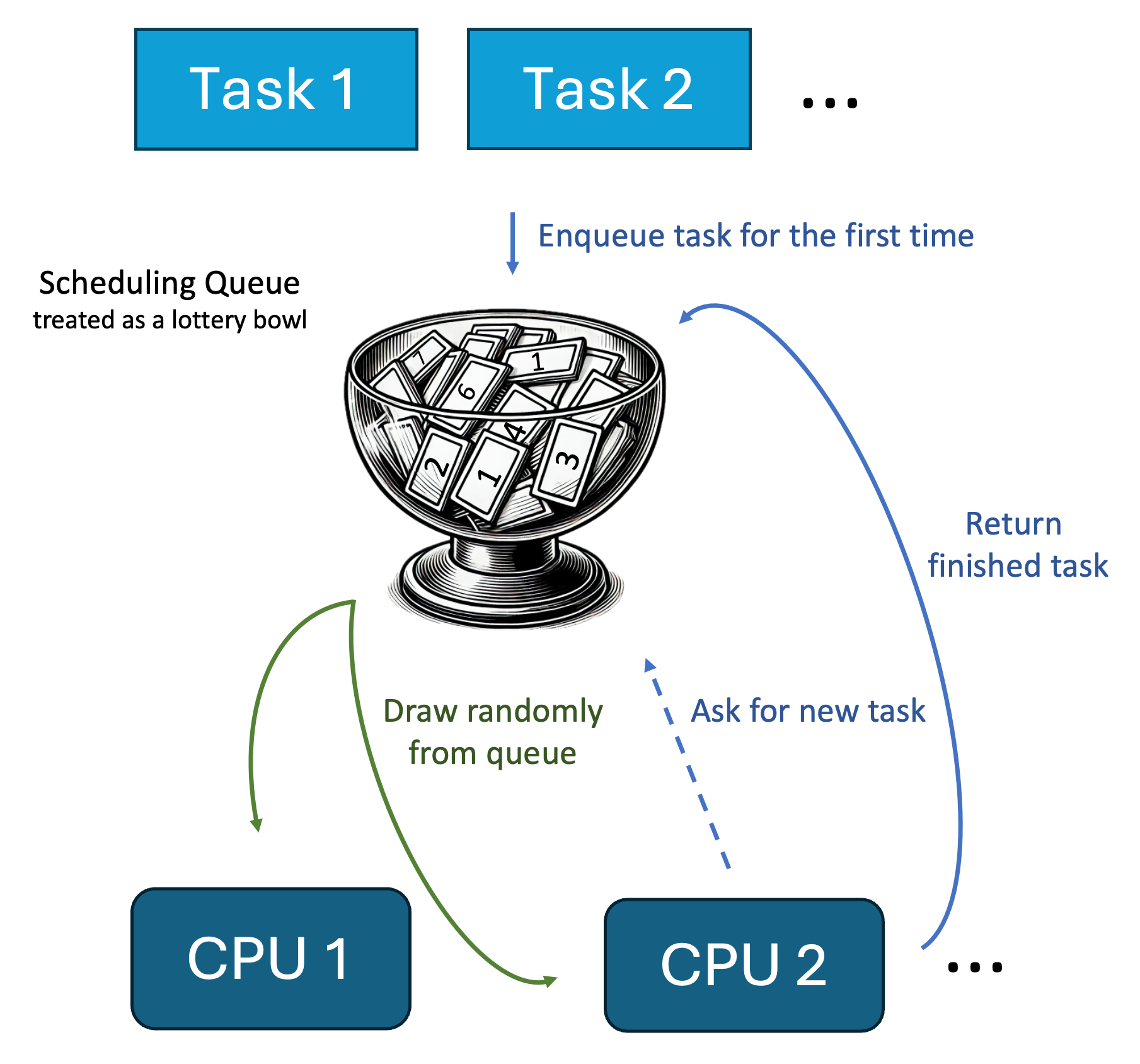
This is a truly random scheduler, making it great for testing applications with random scheduling orders. This is why it’s a great addition to the taskcontrol project.

You might have wondered about the title of my blog post, “Real life practice in lottery scheduling.” the whole point of writing the post was to detail my idea of using lottery scheduling for learning. I don’t want to keep this from you, so here’s the rest of the post:

But how could I use this algorithm in practice?

I take a stack of blanko cards, each card worth around 2 hours of learning time, and assign them to each of my courses. E.g. the course operating systems gets 3 cards, out of the 25 cards that now make up my week.

Now, when I’ve time to learn, I pick a card out of the shuffeled card stack which then tells me to learn about 2 hours e.g. for my theoretical computer science course.

This “practical exercise” in operating systems will hopefully boost my learning – and of course is funny way to learn, as I never know what I’m going to learn. Later, I probably also could use it to ensure that I’m blogging more regularly here and progress with my compiler project.

Real life practice in lottery scheduling

It was a great idea, and I tried using it for a couple of days, but this method of learning is highly impractical when you don’t want to force yourself to learn and instead learn the topics that interest you at the moment (or for which the exam is the closest).

Simplified Algorithm

The original paper introducing lottery scheduling is “Lottery Scheduling: Flexible Proportional-Share Resource Management” by Carl A. Waldspurger and William E. Weihl. In this paper they present a more complex variant, with ticket transfers, inflation, and currencies, but they also give a simplified algorithm:

A straightforward way to implement a centralized lottery scheduler is to randomly select a winning ticket, and then search a list of clients to locate the client holding that ticket. This requires a random number generation and O(n) operations to traverse a client list of length n, accumulating a running ticket sum until it reaches the winning value.

Lottery Scheduling: Flexible Proportional-Share Resource Management

Advantages and Disadvantages

The same paper also gives us the main advantages of the scheduling policy:

Since any client with a non-zero number of tickets will eventually win a lottery, the conventional problem of starvation does not exist. The lottery mechanism also operates fairly when the number of clients or tickets varies dynamically. For each allocation, every client is given a fair chance of winning proportional to its share of the total number of tickets. Since any changes to relative ticket allocations are immediately reflected in the next allocation decision, lottery scheduling is extremely responsive.

Lottery Scheduling: Flexible Proportional-Share Resource Management

Albeit having some nice properties, the policy was introduced in 1994 and since then mostly lives in the curriculum of operating systems courses at universities, never being shipped with mainstream operating systems. However, implementations exist, like implementation in the Linux Kernel in San Luis Obispo’s master thesis. This thesis also gives the major disadvantages:

Specifically, the lottery scheduler’s CPU bound process bias can unfairly penalize interactive loads. Interactive profile processes exhibit uneven performance when running in parallel with CPU bound loads.
Certainly in my implementation, the classic compensation ticket function, as devised by Waldspurger and Weihl (1994), is not sufficient to meet the requirements of interactive loads. […]

This research finds that the order in which processes win the lottery is not
exactly in proportion to the distribution of lottery tickets in the short term. The random nature of the lottery results in an uneven pattern of wins and thus of CPU distribution when viewed over very short periods of time. In the lottery scheduler, the only notion of priority is the relative ratio of lottery ticket allotments. Thus it is possible for an interactive type process that may be deemed as high priority by another scheduler, to lose multiple consecutive lotteries while in possession of a superior ticket ratio.

LOTTERY SCHEDULING IN THE LINUX KERNEL: A CLOSER LOOK

This is consistent with my own observations. But be aware that both the FIFO scheduler from my last blog post and the lottery scheduler implemented in the following are based on their preemptive variant so that the scheduler allows every task to only run a few hundred microseconds to milli-seconds in a row before a new task is scheduled. Otherwise, interactive processes would exhibit even worse responsiveness.

But how can you try the lottery scheduler yourself?

Usage

As mentioned before, I implemented the lottery scheduler in the taskcontrol project. So follow the install instructions from the README (Linux Kernel 6.12+ and libbpf as requirements).

Running the scheduler is then pretty easy:

./scheduler.sh --scheduler=lottery

Now, on to the implementation with hello-ebpf:

Implementation

For the implementation, we first extend the TaskSetting record to accommodate the lottery priority (or number of lottery tickets):

@Type
record TaskSetting(boolean stop, @Unsigned int lotteryPriority) {
    public TaskSetting {
        if (lotteryPriority <= 0) {
            throw new IllegalArgumentException(
            "lotteryPriority has to be positive, got " + lotteryPriority);
        }
    }
}

A negative number of tickets is forbidden, and giving a task zero tickets prevents it being considered from scheduling (so stop == true and lotteryPriority == 0 are equivalent)

The main part of the implementation is in the LotteryScheduler class. I won’t bother you with setting up the task and task group settings map, as this is equivalent to the FIFOScheduler. This is also true for the enqueue implementation, but I present it here for the sake of completeness:

@Override
public void enqueue(Ptr<TaskDefinitions.task_struct> p, long enq_flags) {
    var sliceLength = ((@Unsigned int) 5_000_000) / 
                      scx_bpf_dsq_nr_queued(SHARED_DSQ_ID);
    scx_bpf_dispatch(p, SHARED_DSQ_ID, sliceLength, enq_flags);
}

So we use a scheduling time slice of a maximum 5ms, inversely scaled by the number of waiting processes to improve the usability on modern systems a dynamic (and typically high) number of tasks.

We then define three helper functions to access the properties and stop the property of every task quickly (keep in mind that this is either defined for the task or its task group or not at all):

@BPFFunction
@AlwaysInline
public void getSetting(Ptr<TaskDefinitions.task_struct> p, Ptr<TaskSetting> out) {
    // we cannot return the setting object directly, because eBPF
    // does only support scalar return values upto 64 bit
    var taskSetting = taskSettings.bpf_get(p.val().pid);
    if (taskSetting != null) {
        out.set(taskSetting.val());
        return;
    }
    var groupSetting = taskGroupSettings.bpf_get(p.val().tgid);
    if (groupSetting != null) {
        out.set(groupSetting.val());
        return;
    }
    out.set(new TaskSetting(false, 1));
}

@BPFFunction
@AlwaysInline
public int getPriorityIfNotStopped(Ptr<TaskDefinitions.task_struct> p) {
    TaskSetting setting = new TaskSetting(false, 1);
    getSetting(p, Ptr.of(setting));
    if (setting.stop()) {
        return 0;
    }
    return setting.lotteryPriority();
}

And also the simplified version of tryDispatch:

@BPFFunction
@AlwaysInline
public boolean tryDispatching(
  Ptr<BpfDefinitions.bpf_iter_scx_dsq> iter, 
  Ptr<TaskDefinitions.task_struct> p, int cpu) {
    // check if the CPU is usable by the task
    if (!bpf_cpumask_test_cpu(cpu, p.val().cpus_ptr)) {
        return false;
    }
    return scx_bpf_dispatch_from_dsq(iter, p, 
        SCX_DSQ_LOCAL_ON.value() | cpu, SCX_ENQ_PREEMPT.value());
}

It is more straightforward than the version for the FIFO scheduler, as we check whether or not the task can be scheduled at all in the dispatch function that calls tryDispatch.

The implementation of dispatch is straightforward: We first compute the sum of priorities (or tickets) for all tasks in the queue, pick a random number between 0 and the sum, and then iterate so long over the queue, subtracting the priority of each task from the sum, till the sum isn’t positive. We take the task when this occurs. Sadly, The implementation is not yet in Java because of the lack of support for bpf_for_each in hello-ebpf, but I hope to find time to rectify this in the future. The actual implementation for dispatch is as follows:

@Override
public void dispatch(int cpu, Ptr<TaskDefinitions.task_struct> prev) {
    String CODE = """
        s32 this_cpu = bpf_get_smp_processor_id();
        struct task_struct *p;
        int sum = 0;
        bpf_for_each(scx_dsq, p, SHARED_DSQ_ID, 0) {
           sum += getPriorityIfNotStopped(p);
        }
        int random = bpf_get_prandom_u32() % sum;
        bpf_for_each(scx_dsq, p, SHARED_DSQ_ID, 0) {
            int prio = getPriorityIfNotStopped(p);
            random -= prio;
            if (random <= 0 && prio > 0 && tryDispatching(BPF_FOR_EACH_ITER, p, this_cpu)) {
                return 0 ;
            }
        }
        """;
}

Conclusion

Implementing another scheduler in my taskcontrol tool showed how easily sched-ext can be used to implement simple scheduling algorithms known from operating system courses. This could make sched-ext (and, in extension, hello-ebpf) a great tool for education. Allowing students to directly implement schedulers they see in class, rather then just learning about them.

But this blog post also shows that hello-ebpf is in dire need of supporting macros, like bpf_for_each to be able to write the schedulers in pureish Java again, without inline C code. Let’s see whether I can achieve this till the next blog post.

Thank you for joining me on this journey to bring eBPF and sched-ext to the Java world. See you in two weeks for more on scheduling and eBPF.

P.S.: I’ll be giving the introductory sched-ext talk in the eBPF dev room at FOSDEM 2025; say hi if you’re also there, and get your own sched-ext sticker.

P.P.S.: I wish you all a great Christmas time (on the off chance that I don’t write a blog post next week).